[OC] Prime Distribution in the Sacks Spiral – 60,000 Integers, Euler’s Polynomial Highlighted

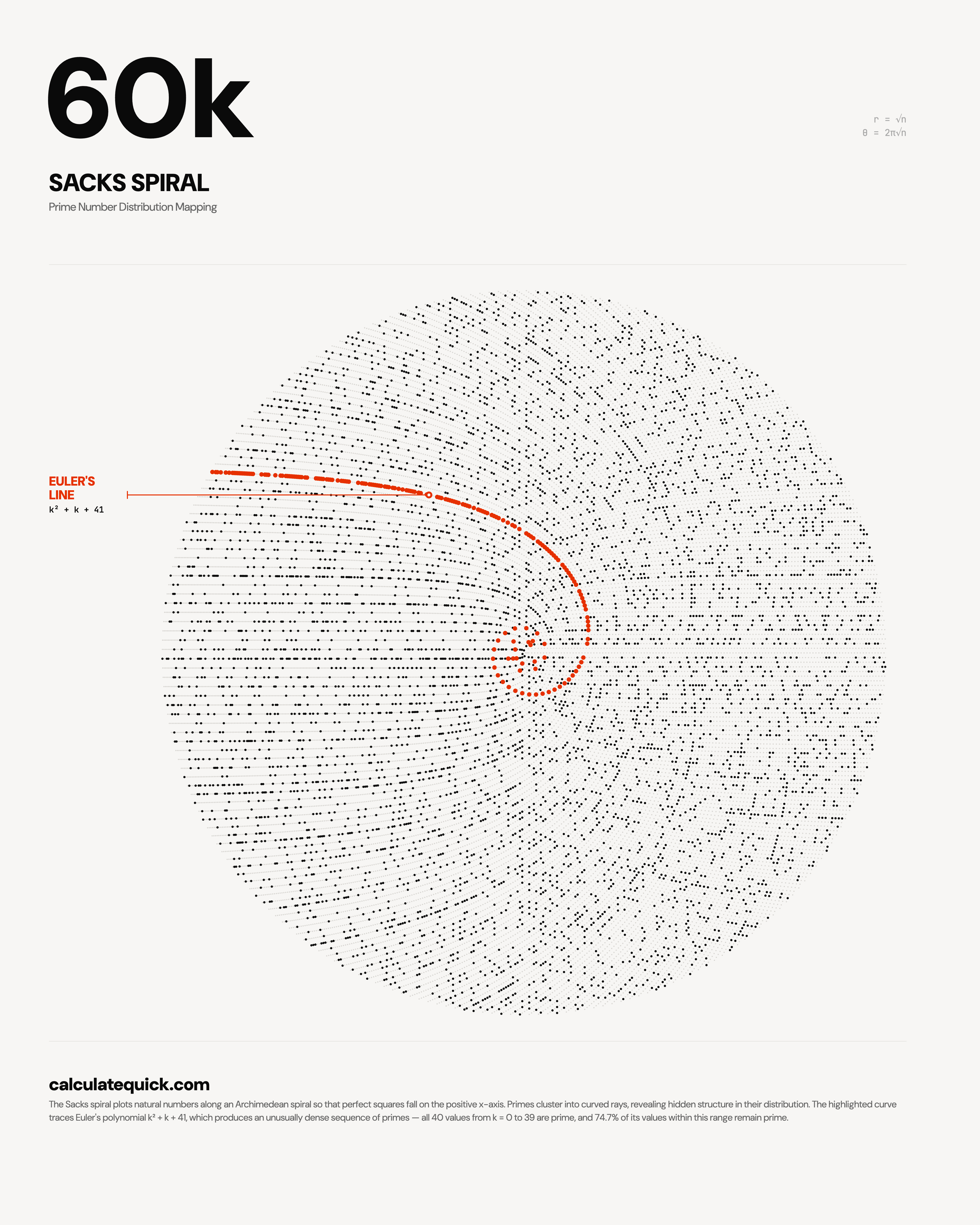
Source: CalculateQuick (visualization), Robert Sacks (1994/2003), Euler's prime-generating polynomial (1772). Prime density reference: Zagier, "The first 50 million prime numbers," Mathematical Intelligencer Vol. 1, 1977.

Tools: Python with NumPy for sieve computation and Matplotlib for polar rendering. Archimedean spiral coordinates r = √n, θ = 2π√n. 60,000 integers plotted; primality via Sieve of Eratosthenes (validated against trial division for full range).

The orange curve traces Euler's polynomial f(k) = k² + k + 41, which famously produces primes for every integer k from 0 to 39 – and maintains a 74.7% prime rate across the 245 values within this range. First composite value occurs at k = 40, yielding 1681 = 41².