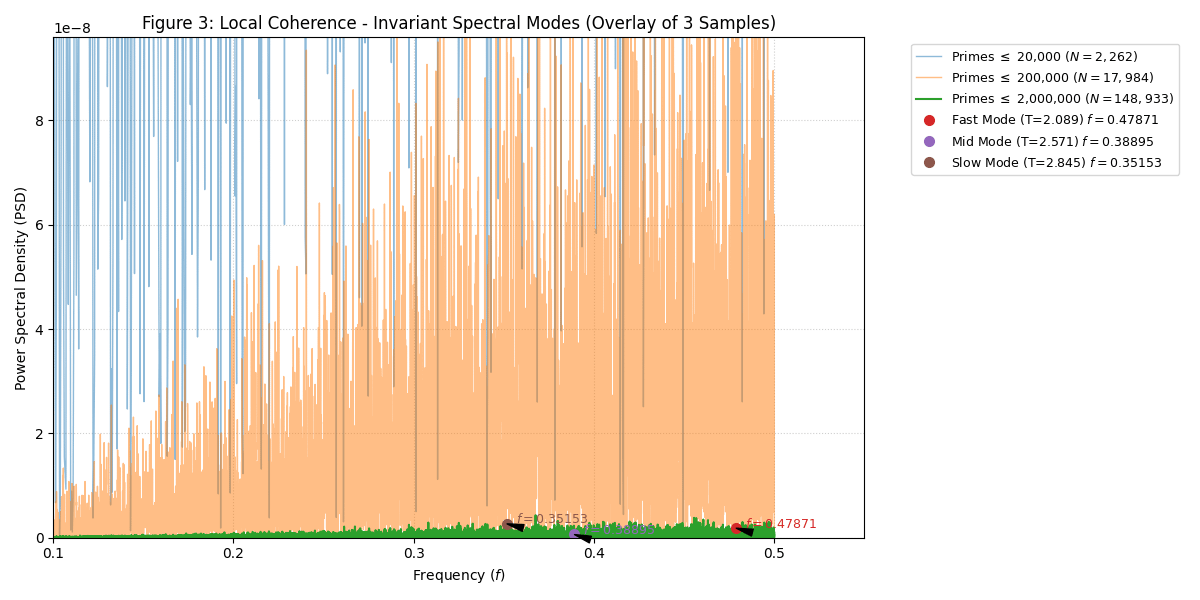
I’ve been exploring prime numbers from a different angle — literally.
Each pair of consecutive primes (pn,pn+1) is treated as a vector from the origin, and I measure the angle between them:
α=arctan(pn/pn+1)
The change in this angle, Δα, creates a time-series signal.
When you run an FFT on Δα across the any sample of primes, you get consistent peaks that suggest an underlying wave structure in how primes “turn.” This demonstrates local coherence and invarient structure in the prime number sequence.
All code, data, and figures are open source here:
GitHub: Prime-Wave Duality
Zenodo DOI: 10.5281/zenodo.17469196
I’m not claiming a proof — just sharing something that looked too structured to ignore.
Would love thoughts from data analysts or math folks who see patterns where others see chaos.
by forwantoftheprice
5 Comments
why did you plot in loglog to seen the whole dynamics?
The figure was generated by the prime number sequence and FFT analysis. The analysis and image were generated by Python code which executed the analysis. That code as well as other data and reporting can be found at [https://github.com/allen-proxmire/prime-wave-duality](https://github.com/allen-proxmire/prime-wave-duality)
A bit like ulam spirals
https://en.wikipedia.org/wiki/Ulam_spiral
I don’t see what you’re saying are the “consistent peaks”.
I have a true story about something like this. I got very weird for a few days and tried to understand the density of numbers with unique prime factors (no repeating primes). I used GPT to create an XLS that would do the calculation over any mammoth segment of the number line, and it seemed to converge on a ratio! Something about this irked me, and I had a dream that there was Pi in there somewhere. Sure enough it was a fraction that included Pi. I don’t remember the specifics! But then I watched a YouTube video that explained the relationship between the density of primes and Pi. It was nuts, but it made sense. There’s a hidden circle! Anyway – good luck with this.